Time-related LSTM
其实之前有面试被问到过类似怎么融合时间的问题。当时见的还比较少,直接说了根据时间抽样,现在看来正确答案貌似应该是这个。
论文意图和背景
长话短说,其实就是要在lstm中加入时间的概念
传统的LSTM
$ i_t = \sigma_{i}(x_tW_{xi} + h_{t-1}W_{hi} + w_{ci} \odot c_{t-1} + b_i ) $
$ f_t = \sigma_{f}(x_tW_{xf} + h_{t-1}W_{hf} + w_{cf} \odot c_{t-1} + b_f) $
$ c_t = f_t \odot c_{t-1} + i_t \odot \sigma_{c}(x_tW_{xc} + h_{t-1}W_{hc} + b_c) $
$ o_t = \sigma_{o}(x_tW_{xo} + h_{t-1}W_{ho} + w_{co} \odot c_t + b_o ) $
$ h_t = o_t \odot \sigma_{h}(c_t) $
Phased LSTM
Phased LSTM增加了time gate。开启和关闭这个门由三个参数决定。
$ c_t $和 $ h_t $ 仅仅在门开启的时候允许通过。$ \tau $ 控制了震荡的时间。$ \tau_{on} $ 控制了开相对于整个时间周期的比例。
$ s $ 控制了相位的偏移。这些参数都是可以学习的。
$ \phi_{t} = \frac{(t-s) mod \tau }{ \tau } $
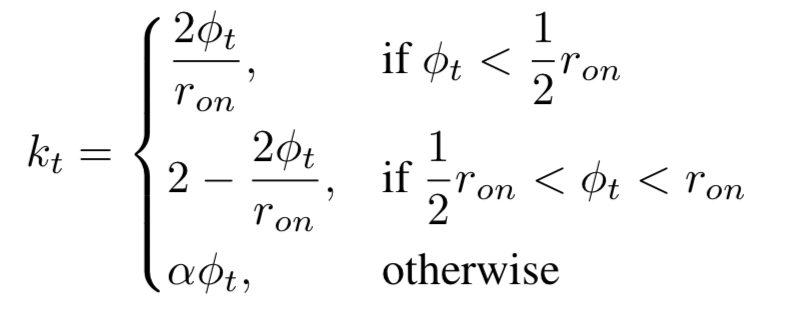 所以phased_lstm的公式还需要time gate的更新:
所以phased_lstm的公式还需要time gate的更新:
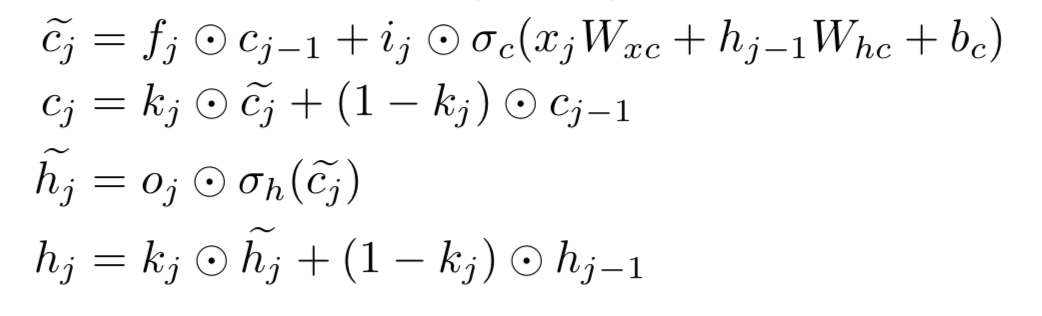 Phased LSTM还有一个好处, 它能更好地保持初始信息。
传统的lstm:
Phased LSTM还有一个好处, 它能更好地保持初始信息。
传统的lstm:
$ c_n = f_n \odot c_{n-1} = (1-\epsilon) \odot (f_{n-1} \odot c_{n-2} ) = … = (1-\epsilon)^n \odot c_0 $
相反地, 在gate关闭的时候, Phased LSTM可以很好地保存信息。
Phased LSTM实验结果
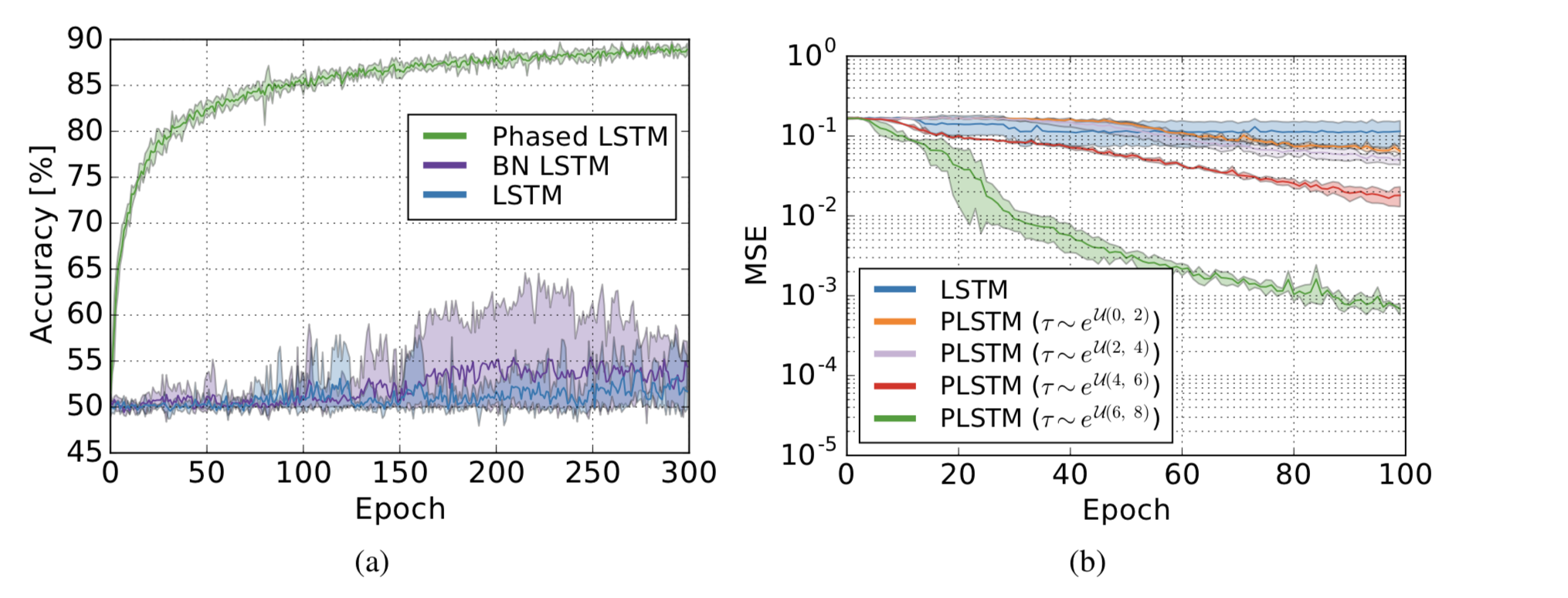 可以看到在一些数据集上其实效果远胜传统的lstm,具体可查看原论文。
可以看到在一些数据集上其实效果远胜传统的lstm,具体可查看原论文。
Phased LSTM缺点
当然, Phased LSTM也有一些缺点。
- 它仅仅考虑时间点的建模,而没有考虑时间间隔建模。在推荐系统中,Phased LSTM仅仅对考虑了用户的活动状态而未考虑用户的静止状态(因为Phased LSTM设置了静止状态)。
- 并不能区分短时兴趣和长期兴趣的影响。
Time LSTM
Time LSTM的提出就是为了克服Phased LSTM的问题。给定:
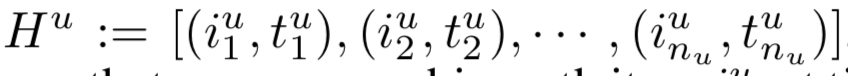 实际建模时会把单点的时间转换为时间间隔建模。
实际建模时会把单点的时间转换为时间间隔建模。
Time LSTM变体
Time LSTM变体1
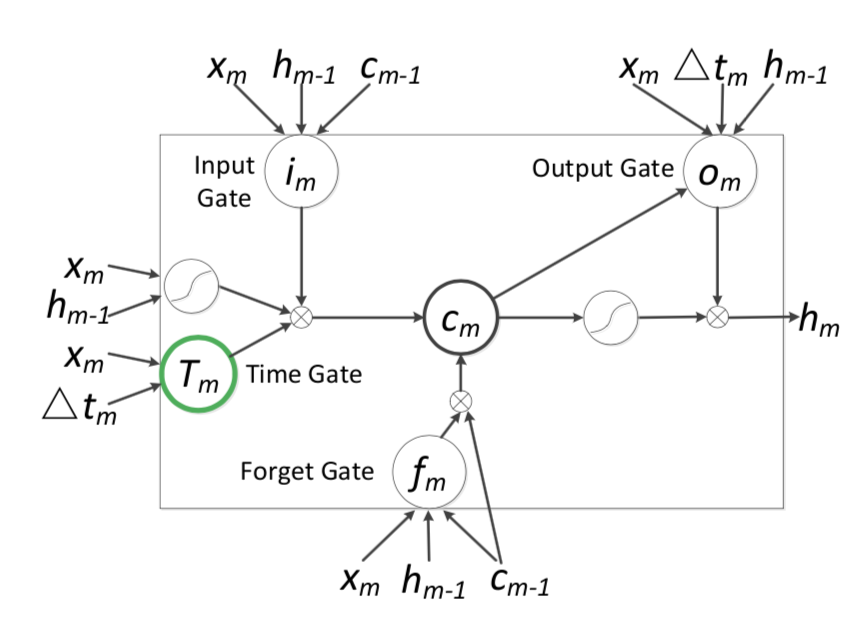
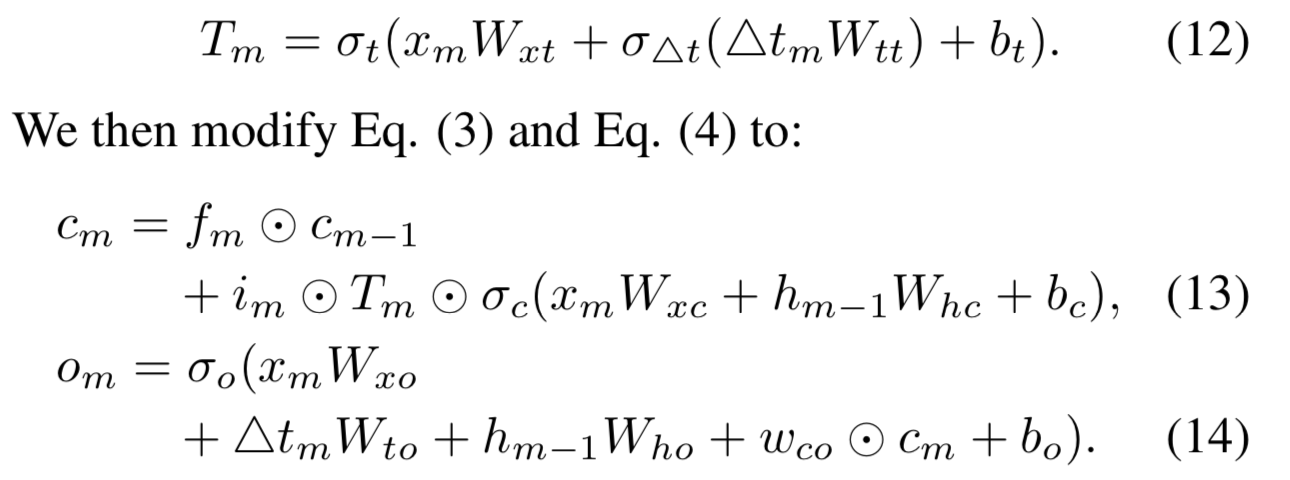 这是Phased LSTM最简单的改变,仅仅是把时间点换成了时间间隔,非常清晰易懂。
这是Phased LSTM最简单的改变,仅仅是把时间点换成了时间间隔,非常清晰易懂。
Time LSTM变体2
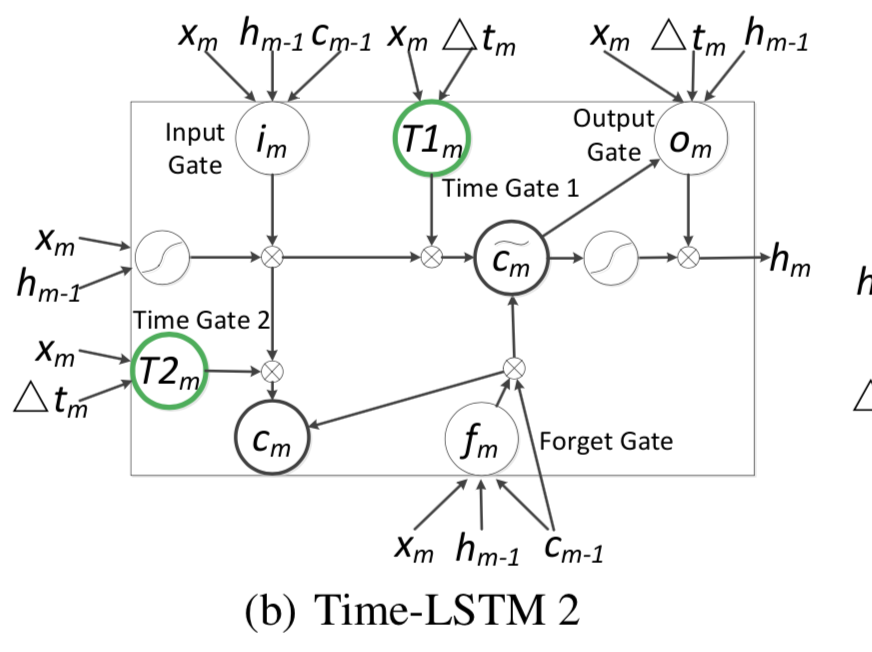
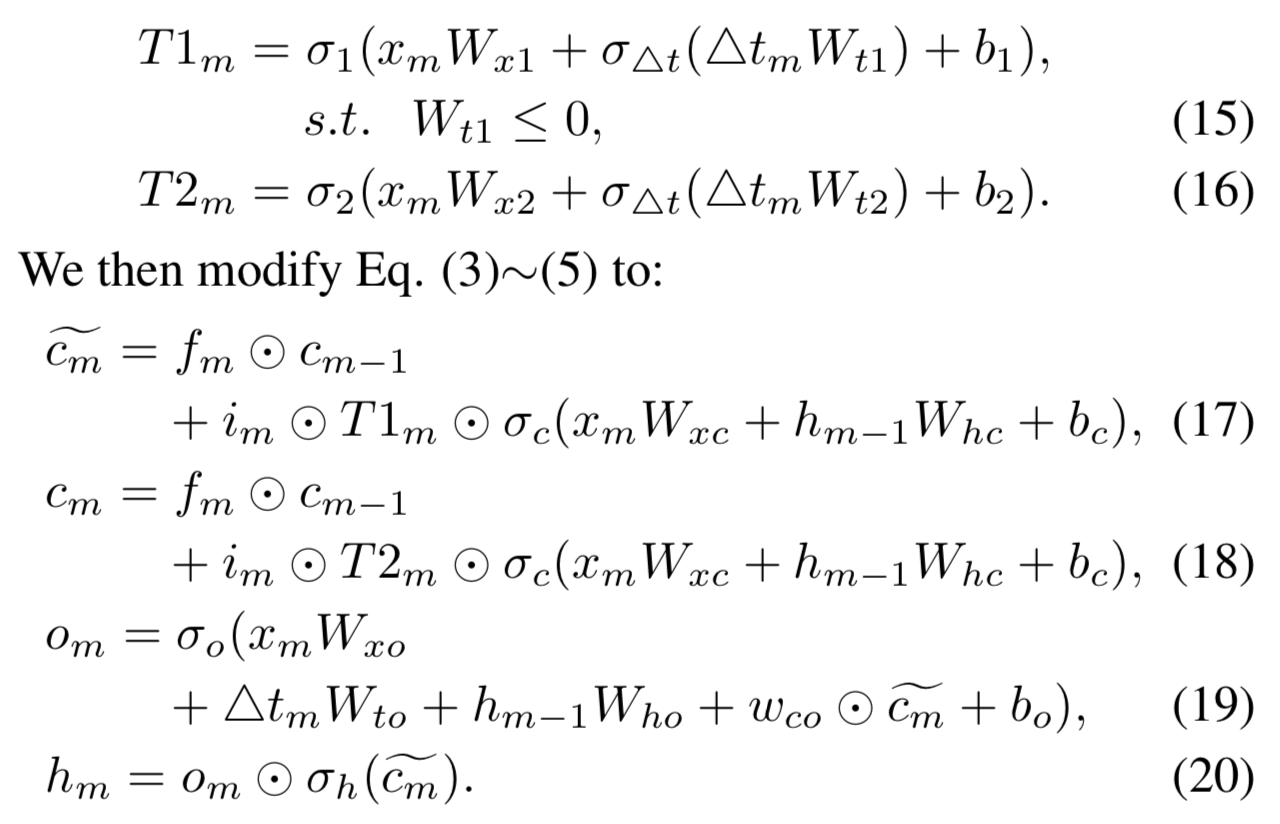 使用了2个Time gate。Time gate1主要用来利用现在的时间间隔来进行现在物品推荐,Time gate2主要用来存储时间间隔为以后的推荐准备。
使用了2个Time gate。Time gate1主要用来利用现在的时间间隔来进行现在物品推荐,Time gate2主要用来存储时间间隔为以后的推荐准备。
Time LSTM变体3
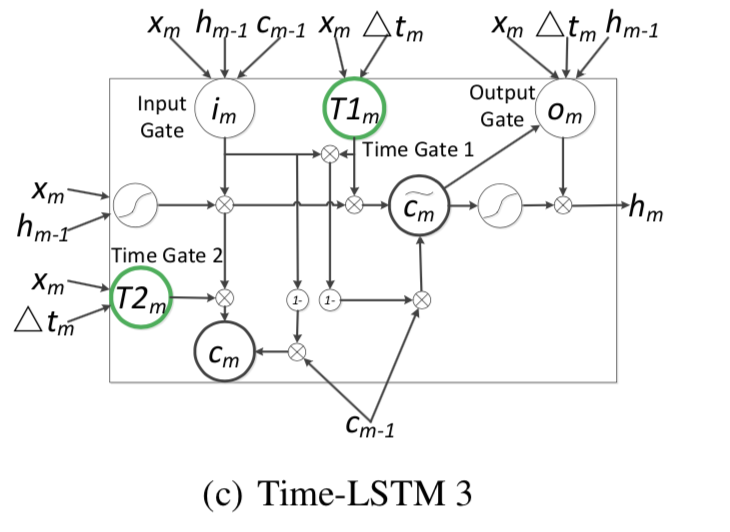
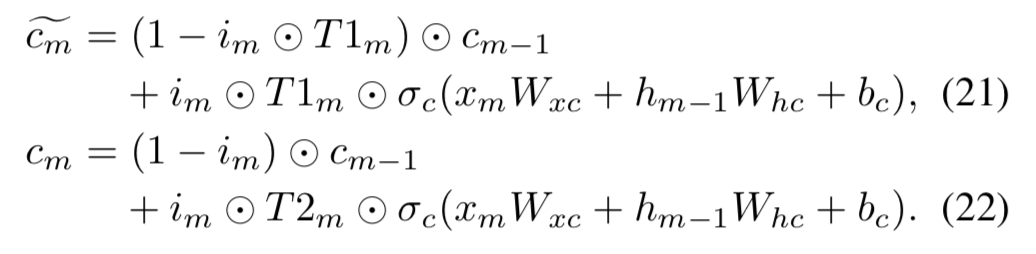 Time LSTM变体3用了耦合的输入门和忘记门。
Time LSTM变体3用了耦合的输入门和忘记门。
Time LSTM实验结果
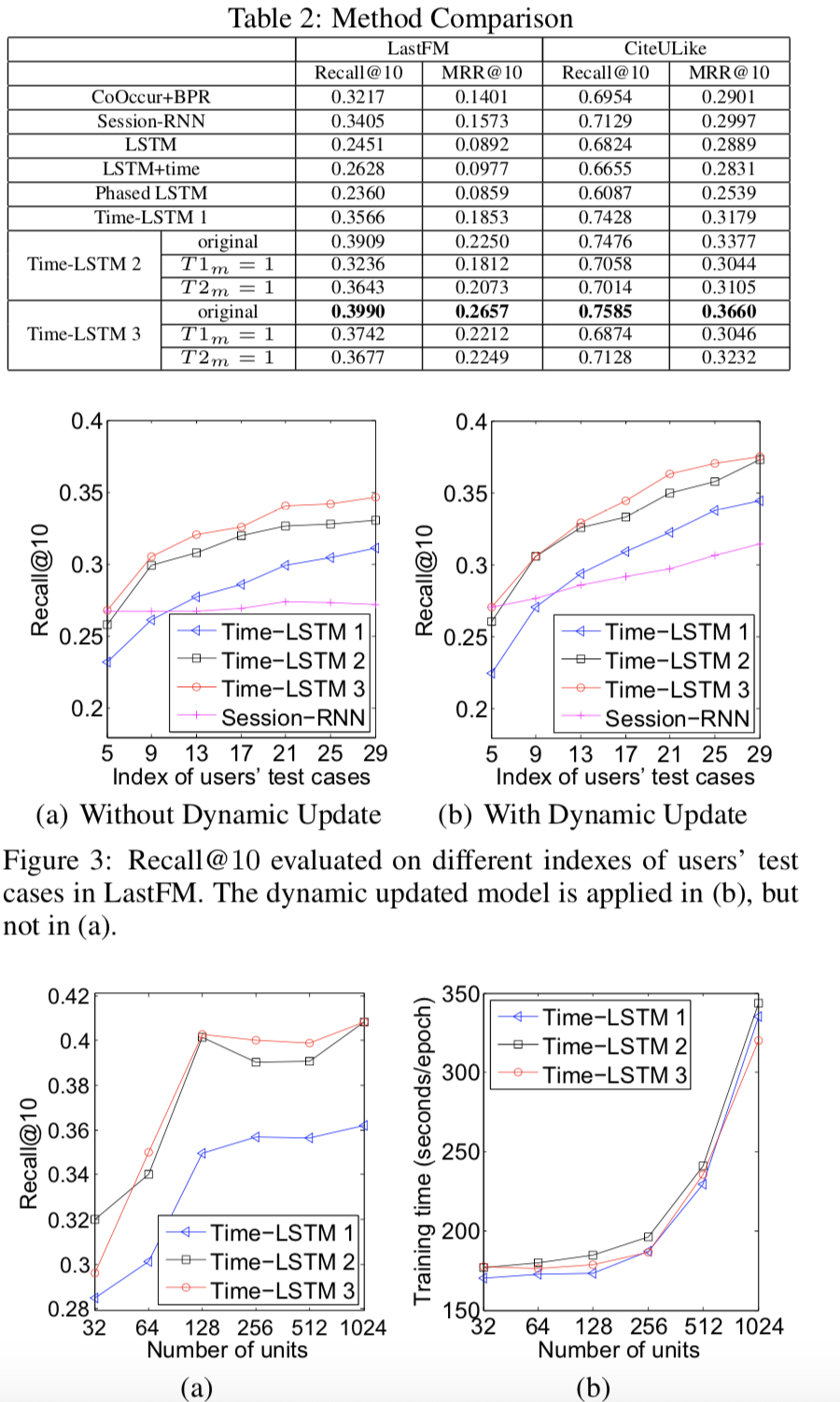 可以看到Time LSTM确实在效果上优于之前的Time-related LSTM方法
可以看到Time LSTM确实在效果上优于之前的Time-related LSTM方法
Phased LSTM torch开源实现
1 | import math |
Content-aware Neural Hashing for Cold-start Recommendation
这是一篇sigir2020推荐系统的文章。
论文背景:
通过学习item的hashcode表示来进行冷启动。基于协同过滤和内容的推荐系统是很主流的方法。
协同过滤的缺点:
对于未见过的item,标准的协同过滤不能学习有效表示。所以基于内容的推荐系统可以补充标准协同过滤的方法。
基于内容的推荐系统的缺点
基于内容(content-aware)hashcode表示个生成和标准item的生成不同,是不必要的并且会限制其泛化性能。
NeuHash-CF
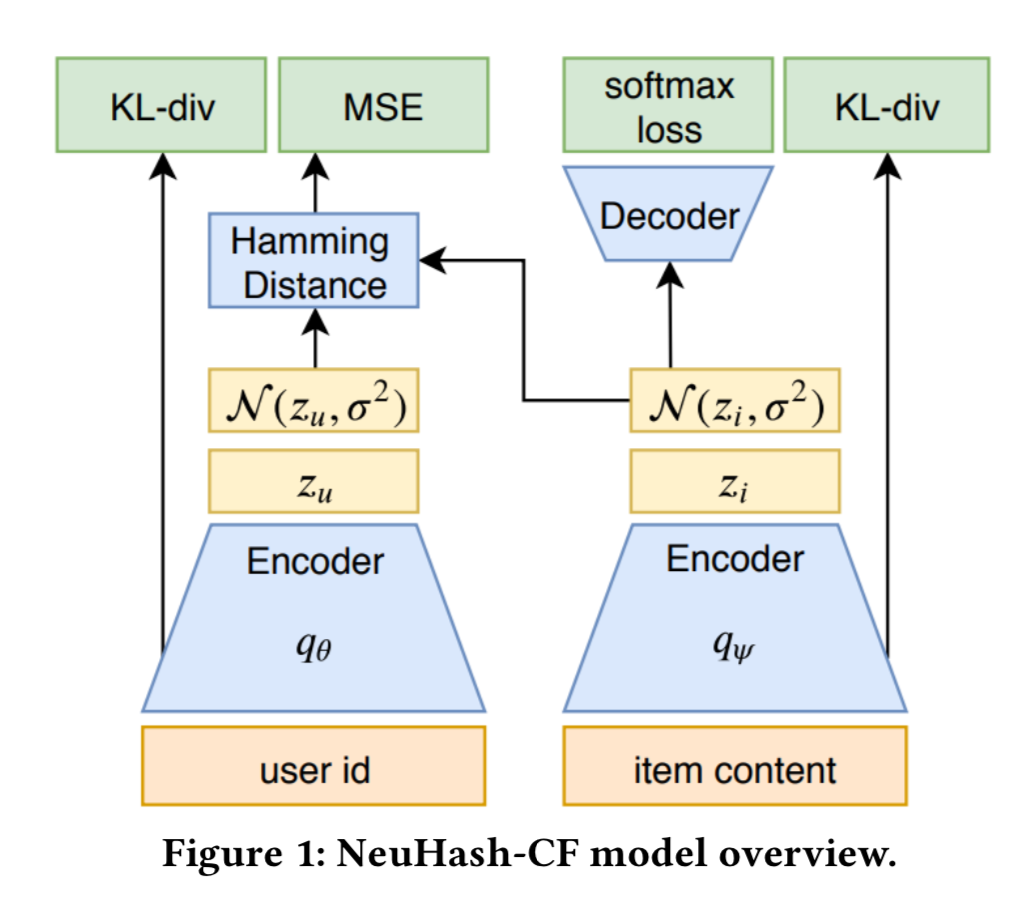
NeuHash-CF有两个encoder来生成item和user的hashcode, 它们连接在变分自编码模型中. 所有的item code都统一生成,不管是否曾经见过。
Variational AutoEncoder
$ p(u) = \prod_{i \in I_u} p(R_{u,i}) $
$ p(i) = p(c_i) + \prod_{u \in U_i } {p(R_{u,i})} $
$ p(c_i) = \prod_{w\in W_{c_i} } p(w) $
$ logp(R_{u,i}) = log \Sigma_{z_i,z_u \in \{ -1,1 \}^m }p(R_{u,i}|z_i,z_u)p(z_i)p(z_u) $
$ logp(c_i) = log \Sigma_{z_i \in \{ -1,1\}^m } p(c_i |z_i)p(z_i) $
上面的公式把content-based推荐和cf推荐进行联合建模。后续的hashcode采样和em优化详细可以看文章。
Encoder Function
item encoding:
$ l_1 = ReLU(W_1(c_i \odot w_{imp} ) + b_1) $
$ l_2 = ReLU(W_2l_1 + b_2) $
item采样概率: $ q_{\phi}(c_i) = \sigma_{(W_3l_3+b_3)} $
user和item类似的情况。
Decoder Function
User-item rating decoding
Item content decoding
Noise infusion for robustness
Combined loss function
$ L = L_{rating} + \alpha L_{content} $
实验结果
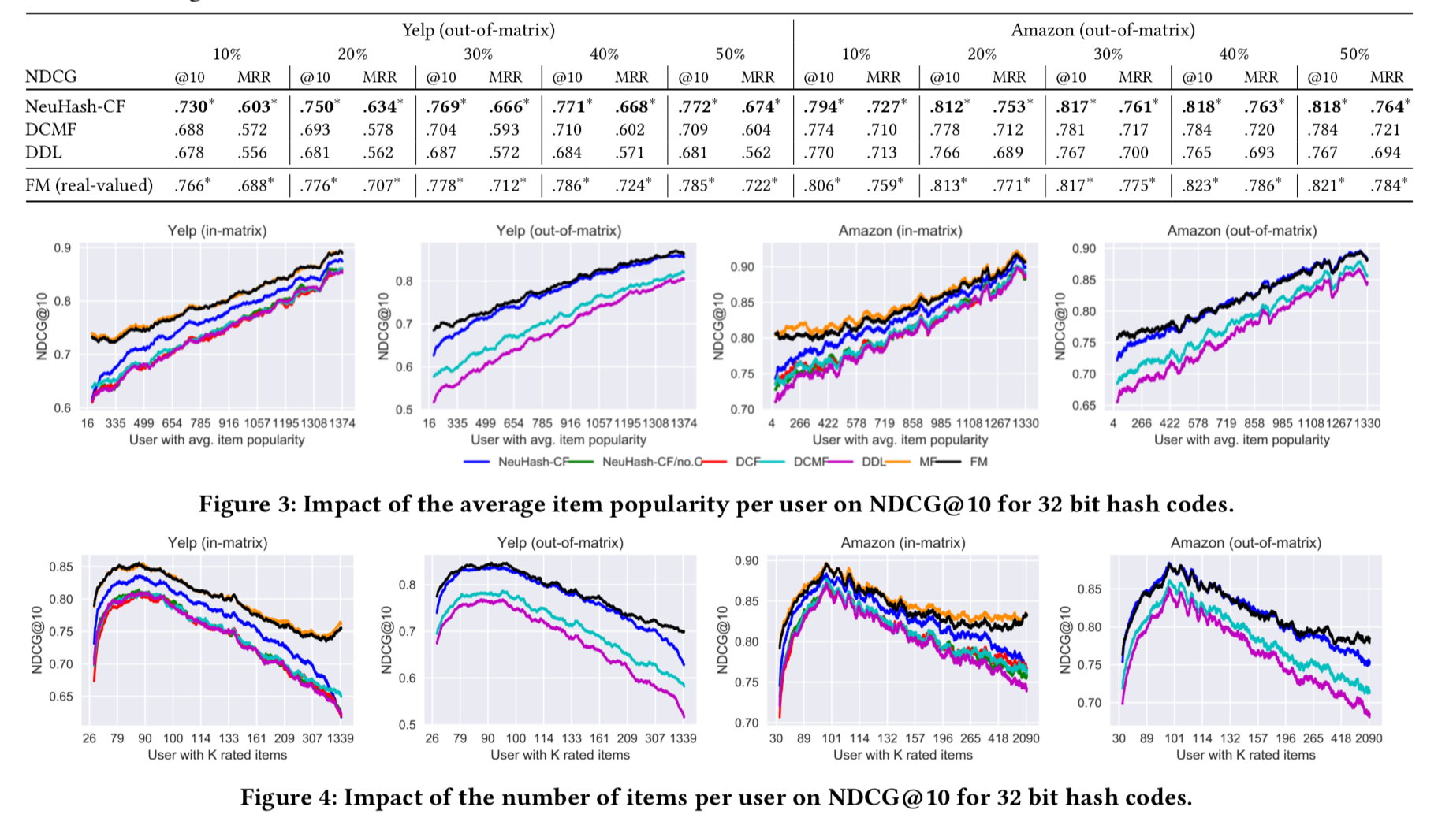
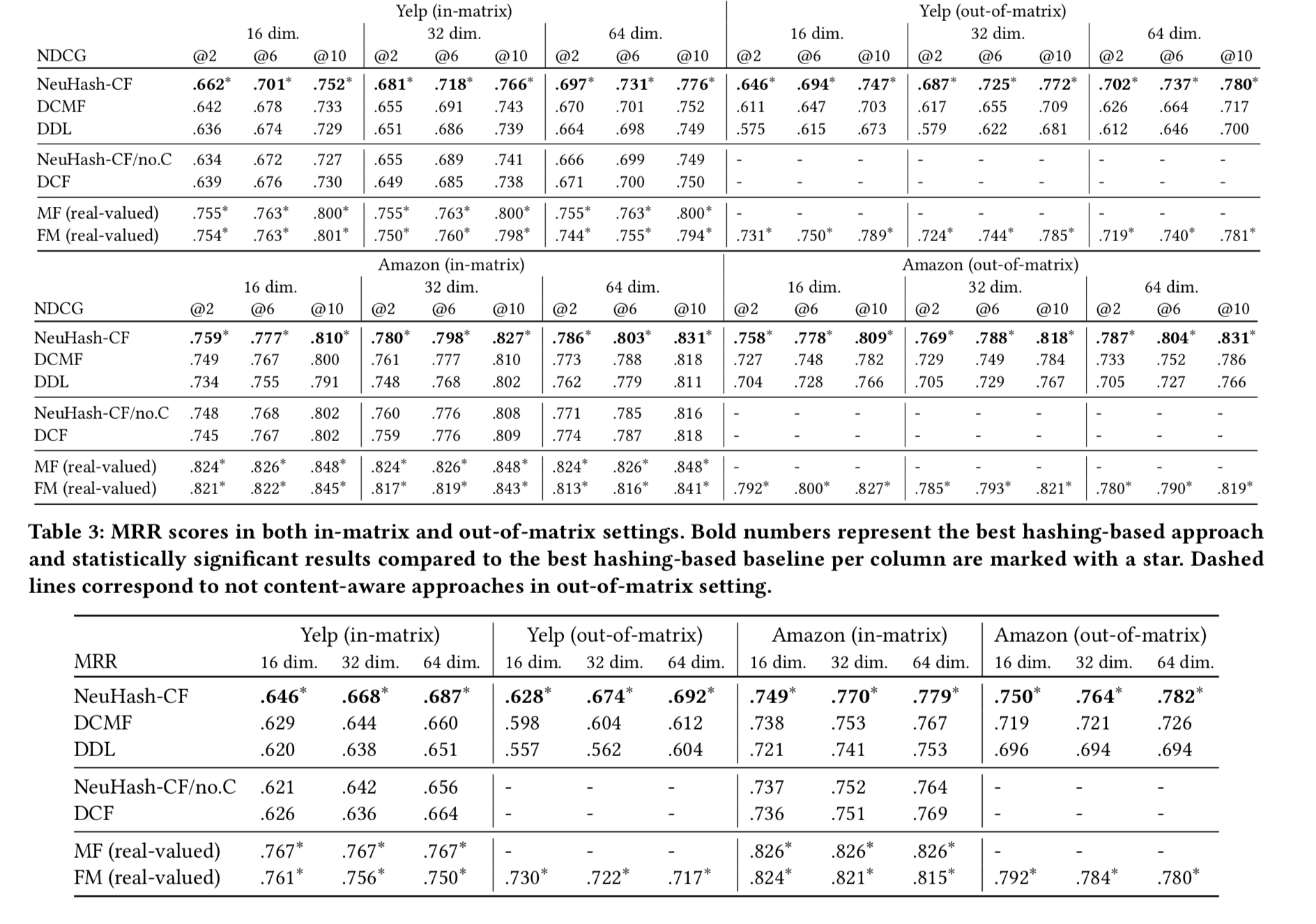
看实验效果感觉还可以。就是建模比较复杂,期待源码。